Problem description
Colebrook & White equation is widely used for calculating the friction factor in turbulent flows. The equation is complicated to be solved by hand, but with nowadays computers we can overcome this difficulty very fast. The equation is written below:
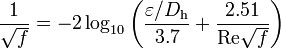
Where:
The Reynolds number is calculated by the following formula:
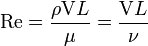
Where:
Solutions
Here we will discuss five different approaches to the above equation. The degree of accuracy differs for each approach, as well as the level of difficulty.
1. Iteration process
If we rewrite the above equation, it will look like this:

By changing the values of friction factor, we can find the solution using the trial and error method. However, this can easily be done in an Excel worksheet using goal seek.
2. Swamee – Jain’s equation
The Swamee – Jain’s equation is used to find the friction factor in a full-flowing circular pipe directly. It is an approximation of the Colebrook & White’s equation.

3. Haaland’s equation
Haaland in 1983 simplified the Colebrook & White’s equation to the following equation:

4. Serghides’ equations
The last two solutions are more complicated since they approach the problem with a set of equations. Serghides’ solution was based on Steffensen’s method. The solution involves the calculation of three intermediate values first and then substituting those values into a final equation.

5. Goudar – Sonnad’s equations
Goudar – Sonnad’s set of equations is the most complicated of all the solutions since there are a lot of intermediate values that should be calculated before the final equation. This set of equations is given below:

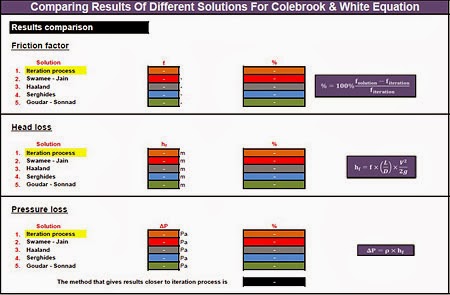
Considering that the iteration process provides the most accurate results, I have developed an Excel workbook to experiment on the other four solutions/methods. So, with this workbook, you can try it yourself and see which approach gives results that are closer to the iteration process results.
How to use it
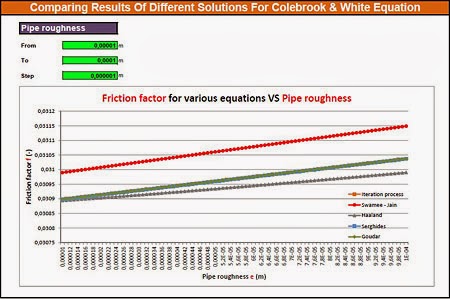
In the first sheet (named “Solutions”) fill all the green cells and press the “Solve Equation” button. If the flow in the pipe is turbulent, the sheet will automatically calculate the friction factor with the five different methods that described above. If you press one of the buttons named “Roughness,” “Diameter,” “Velocity” or “Viscosity” you will be transferred to the corresponding sheet. There you can “play” (loop calculation) with the relevant parameter and see how the results of five methods are affected by the parameter’s change. Furthermore, in every sheet, there is also a chart which depicts the results of your loops.
Downloads
This file can be opened with Excel 2007 or newer. For best results, go to File -> Options -> Formulas tab and put Maximum Iteration = 30,000 (max value is 32,767) and Maximum Change = 0.00001 (or even smaller).
Read also
10 + 1 Ways To Find The Friction Factor In Pipes
Pressure Losses In Piping Systems
Friction Factor Function
Head And Pressure Losses In Pipes


Hi ma65p,
A short answer will be that the most accurate equation depends on the input parameters.
I think that the iterative process gives the best results. Then are probably the Goudar – Sonnad and Serghides' equations. Excluding the iterative process, the results are strongly depended on input parameters (roughness, diameter, fluid velocity etc.), so in some cases maybe the Goudar – Sonnad is better, while on others the Serghides. Because this is unclear, you can run the other sheets of this workbook in order to perform a parametric analysis and see which equation is better for your case.
You can check also this workbook that has more equations.
Kind Regards,
Christos
Thank you for the spreadsheet. However, what was your conclusion as to which approximation was the most accurate?