Introduction
In the past, the fatigue design was based on the attempt of engineers to find the endurance limit of the materials in order to determine the limiting stress below of which the fatigue failure will not take place. Therefore, the testing was only focused on high number of cycles (greater than 10^5 cycles). Although this approach was sensible for many industrial components it led to over-design of components which were subjected to less than 10^5 cycles of operation.
In general, industrial gas turbines usually suffer from low cycle fatigue (LCF). This occurs due to the high load (high stresses) that is applied under few cycles of operation. Some large industrial gas turbines may work for almost a year without stopping for maintenance. But, at every cycle of operation (start-up, operation and shutdown), they may lose almost 10% of their lifetime (due LCF). So, in general, it is not so important the number of times that the load is applied, but the damage that produces when it is applied. Since the damage is associated with the plastic deformation, LCF is frequently called “high strain fatigue”.
In LCF, due to the high stresses, there is a large energy concentration (greater than in high cycle fatigue – HCF) and the material spends only a small percentage of its lifetime in the crack initiation phase (about 10%), whilst most of its lifetime is spent in the crack propagation phase (about 90%).
The material of the component that is subjected to very high load it is possible to deform plastically and to redistribute the load. If this does not happened (no plastic deformation by the load), the load will just stretch the elastic line (up and down). In that case LCF will not take place and the fatigue life of the component could be estimated using the Goodman’s diagram (elastic type analysis). However, if the plastic strain εp is high enough, there will be some plastic deformation in the second part of the cycle. The material and the load condition will be responsible for the effects that will have the following cycles on the component.
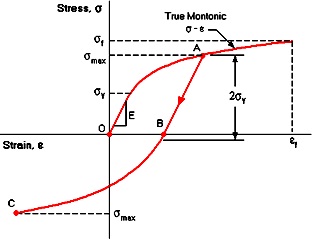
By reversing the loading process (unloading the specimen), the stress-strain relationship will reduce according to the linear segment AB, which has a slope equivalent to the elastic modulus E. If then a compressive load –σmax is applied to the specimen the material will yield at a stress level which is less than the yield stress σY.
If the loading process which was shown in figure 1 continues from –σmax to +σmax, a hysteresis loop will be created. This loop determines one fatigue cycle in the strain-life method. It should be pointed out that stress and strain amplitudes are the half of the corresponding ranges. The area that is included in the loop is the energy per unit volume dissipated during a cycle.
Figure 2: Typical hysteresis loop in the stress-strain curve [1].
The stress-strain response of a material that it is subjected to strain-controlled cyclic loading may change as the number of applied cycles increasing. The material is cyclically hardened when the maximum stress increases at every cycle, whereas is cyclically softened when the maximum stress decreases. Finally, if the maximum stress is constant, the material is cyclically stable. Any transient behaviour of the material tends to be stabilized after a few cycles, usually less than 10% of the total life.
Equations
The cyclic stress-strain curve can be compared with the monotonic stress-strain curve in order to determine the effects of cyclic loading. The cyclic stress-strain curve, as the monotonic stress-strain curve, includes both elastic and plastic strains:
The cyclic stress-strain curve equation is the same with the monotonic stress-strain equation, apart from the power law constants which are different:
Where K’ is the cyclic strength coefficient and n’ is the cyclic strain hardening exponent.
The results of LCF tests are usually presented in plots that have as axes the cycles to failure (Nf) and the total strain range (ΔεΤ). Manson recommended that both strain components produce straight lines when they are plotted logarithmically against Nf. So, he evolve a method (“universal slope method”) based on the Manson-Coffin relationship. Again, the initial point of this method was the assumption that the total strain range is the sum of plastic and elastic strains (strain-life curve).
Basquin, in 1910, suggested that the elastic component could be modelled by a power relationship, which results in a straight line on a logarithmical plot. The Basquin’s equation can be written as:
Where εe is the elastic component of the cyclic strain amplitude, σa is the cyclic stress amplitude, σ’f is the fatigue strength coefficient, Nf is the number of cycles to failure and b is the fatigue strength exponent.
During the 1950’s, Coffin and Manson’s independent experiments shown that the plastic component could also be modelled using a power relationship:
Where εp is the plastic component of the cyclic strain amplitude, ε’f is the fatigue ductility coefficient, Nf is the number of cycles to failure and c is the fatigue ductility exponent.
In 1965, Manson suggested that by summarizing the elastic and plastic components, the strain-life curve can be written as:
In the figure below, the transition life (2Nt) corresponds to the life at which the elastic and the plastic strain ranges are equivalent. Transition life is the point at which LCF and HCF regimes are distinguished. This occurs due to the fact that plastic strains have greater influence on fatigues lives that are below the transition life (corresponding to LCF), while the elastic strains have greater influence above the transition life (corresponding to HCF).
It should be highlighted that at long fatigue lives the fatigue strength (σ’f/E) is responsible for the fatigue performance, while the strain-life and stress life approaches give similar results. At short fatigue lives the plastic strain dominates and the fatigue ductility (ε’f) controls the fatigue performance. So, the optimum material should have both high strength and high ductility. Usually, there is a trade-off between these two properties and a compromise should be done between the expected load and the strain conditions.
Figure 3: Typical strain-life curve [1].
In order to use the above relationships for fatigue, six fatigue properties of the material are required:
For the value of σ’f a good approximation is the true fracture strength, whereas for the value of ε’f the true fracture is used. Usually, for the most metals the value of b varies between -0.05 and -0.12, while the value of c varies between -0.5 and -0.7. The values of c for the ductile metals (ε’f approximately 1) are closer to -0.7, whereas for the strong metals (ε’f approximately 0.5) are closer to -0.5.
References
The article was based on my M.Sc. progress review:
Samaras C., 2009, “Emissions and lifetime estimation modeling of industrial gas turbines”, M.Sc. Progress Review, Cranfield University, UK.
The figures were found from:
[1] Suria ,O. V., 2006, “A flexible lifing model for gas turbines: Creep and low cycle fatigue approach”, M.Sc. Thesis, Cranfield University, U.K.
Read also




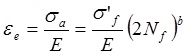





Thank you very much for the information anusha…
It is nice to see you around.
interesting blog
BHM Corporation Incepted in the year 2003.We manufacturing, exporting and supplying of a diversified range of industrial and engineering products and components Plastic Engineering Components