Measuring The Pipe Discharge In Laboratory

Some of the most common instruments for measuring the pipe discharge in laboratory conditions are Venturi, nozzle and orifice meters.  The Venturi meter is consisted of a rapidly converging section, which increases the flow velocity and reduces the pressure. After the converging section, it returns to the original pipe diameter by a gently diverging diffuser-like section.  The discharge is calculated by measuring the pressure differences.  The nozzle meter is similar to Venturi meter, but, instead of converging section, a nozzle is installed inside the pipe, while there is no divergent section. Finally, the orifice meter is a simpler and cheaper arrangement, in which a sharp-edged orifice is fitted concentrically in the pipe.

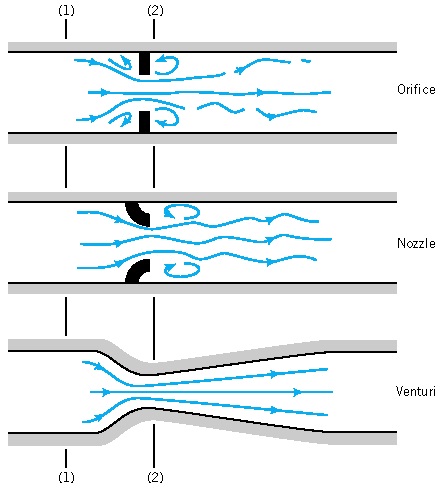
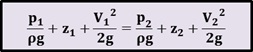The figure above represents the trail of three streamlines inside the instruments. The absence of a converging section in both nozzle and orifice meters causes a greater energy loss in the flow comparing with the Venturi case. This is the reason why Venturi meters are preferred.

All three instruments use the same principles – mathematical equations.  Taking the Venturi meter of the above figure as an example, we apply the Bernoulli equation along the streamline from point 1 to point 2 (throat):

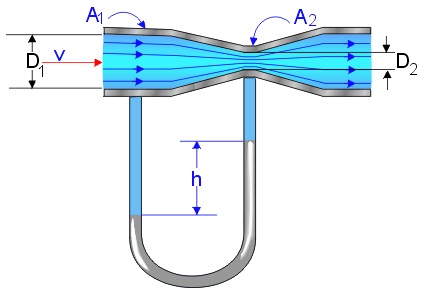
If we consider the fundamental continuity equation, we can write:

  Substituting the V2 in Bernoulli equation, we take:

The ideal/theoretical discharge can be found by multiplying the V1 with area A1. However, due to friction losses the actual discharge will be lower:

Where Cd is the discharge coefficient.
We can relate the terms inside the square brackets with manometer height h by the equation below:

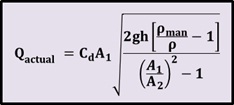
Finally, the combination of the last two equations gives the actual discharge in terms of manometer reading:

The above equation does not include any terms of elevation or orientation of the Venturi meter. This implies that the instrument can be at any convenient angle in order to work.

Limitations/Discussion

The diffuser in a Venturi meter is used to assure the gradual and steady deceleration of the flow after the throat. Moreover, it helps the flow to regain most of its initial pressure (before the instrument). The design angle of the diffuser is strictly between 6 and 8 degrees. The reason for this strict range is that a wider angle will possibly cause flow separation after the throat, while a lower angle would require a long instrument and, consequently, the pressure losses will become significant. Diffuser’s efficiency rarely exceeds 80%.

It should be noted that the above formula was derived by assuming that the flow is steady and there is no energy loss, so as to apply the Bernoulli equation. Although this approximation is convenient for calculation purposes it does not reflect the real situations. The empirical discharge coefficient Cd is introduced in order to denote the difference between ideal and real situation. Typical values of Cd are given below:

Orifice meter: 0.60 – 0.65
Venturi and nozzle meter: 0.98

Since the configuration of an orifice meter is quite abrupt, it is not surprising the fact that it introduces higher energy losses in the flow.

Try yourself

Based on the theory that was described in previous paragraphs I developed a small excel application that can help you can calculate the flow rate and the velocity of a pipe using a Venturi flowmeter.

How to use it

The workbook is quite simple and straightforward. In the sheet “Venturi” fill the necessary values in the green cells and the sheet will automatically calculate the desired parameters. In the auxiliary “Coefficient” sheet you can calculate the discharge coefficient of the instrument. Moreover, there is an auxiliary form – named “Pipe & Fluid Properties” – that will help you insert the input values.

This file can be opened with Office 2007 or newer.