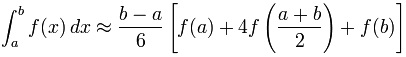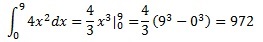Almost two weeks after my initial post about numerical integration in Excel I return to this subject but with a different approach. So, below you will find a custom VBA function that is able to calculate the integral of a given expression – as a function of xi – using the composite Simpson’s rule. Before we go to the function let’s first refer to the original Simpson’s rule.
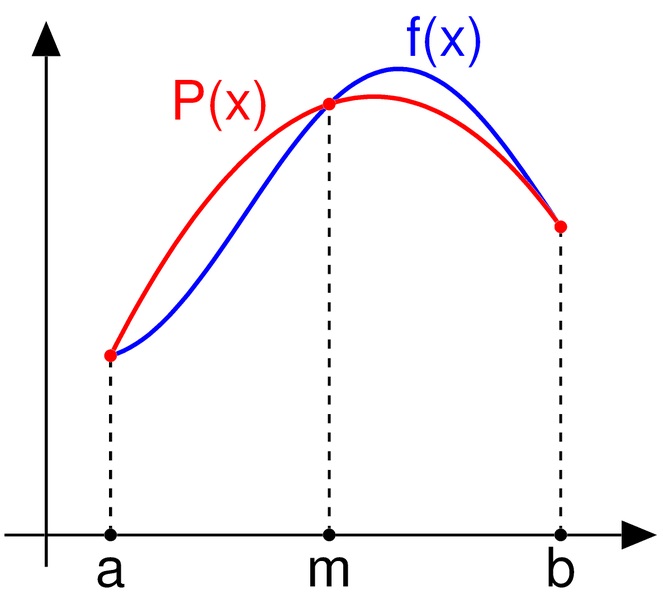
According to Wikipedia, “the Simpson’s rule is a method for numerical integration, the numerical approximation of definite integrals. Specifically, it is the following approximation:
If the interval of integration [a, b] is in some sense “small”, then Simpson’s rule will provide an adequate approximation to the exact integral. By small, what we really mean is that the function being integrated is relatively smooth over the interval [a, b]. For such a function, a smooth quadratic interpolant like the one used in Simpson’s rule will give good results.
However, it is often the case that the function we are trying to integrate is not smooth over the interval. Typically, this means that either the function is highly oscillatory, or it lacks derivatives at certain points. In these cases, Simpson’s rule may give very poor results. One common way of handling this problem is by breaking up the interval [a, b] into a number of small sub-intervals. Simpson’s rule is then applied to each sub-interval, with the results being summed to produce an approximation for the integral over the entire interval. This sort of approach is termed the composite Simpson’s rule.
Suppose that the interval [a, b] is split up in n sub-intervals, with n an even number. Then, the composite Simpson’s rule is given by:
VBA code
Option Explicit
Function SimpsonIntegral(InputFunction As String, Xstart As Double, _
Xend As Double, NumberOfIntervals As Long) As Variant
'----------------------------------------------------------------------------------------------------------
'Calculates the integral of InputFunction using the Composite Simpson's Rule.
'InputFunction is the function to integrate, expressed as a function of "xi".
'Examples: "5*xi + 3", "4*xi^5 + 5*xi^2 + 3*xi + 5", "cos(xi) + tan(xi)".
'Xstart is the initial value of xi.
'Xend is the final value of xi.
'NumberOfIntervals used for integration (rounded up to an even number).
'Bear in mind that this value should be large enough in order to achieve
'a sufficeint degree of accuracy. As a drawback it takes longer computational time to complete.
'Function used directly in a worksheet: =SimpsonIntegral("32*xi^5 + 5*xi^3 + 12*xi + 1"; 0; 100; 1000)
'Note that depending on your settings you might need to change the ";" with ",".
'Function called in VBA: Result = SimpsonIntegral("4*xi^3 + 5*xi^(-1/2) + 5", 1, 10, 100)
'By Christos Samaras
'Date: 23/6/2013
'https://myengineeringworld.net/////
'----------------------------------------------------------------------------------------------------------
'Declaring the necessary variables.
Dim i As Long
Dim TheStep As Double
Dim Cumulative As Double
'Check if the NumberOfIntervals is a valid number.
If NumberOfIntervals < 1 Then
SimpsonIntegral = "The number of intervals must be > 0!"
Exit Function
End If
On Error GoTo ErrorHandler
'Check if the initial and final value of xi are different.
If Xstart = Xend Then
SimpsonIntegral = "Xstart must be different than Xend!"
Exit Function
End If
'Make the NumberOfIntervals even number.
NumberOfIntervals = 2 * NumberOfIntervals
'Calculating the step value.
TheStep = (Xend - Xstart) / NumberOfIntervals
'Calculating the initial value for Xstart.
Cumulative = FunctionResult(InputFunction, Xstart)
'Loop for odd values.
For i = 1 To NumberOfIntervals - 1 Step 2
Cumulative = Cumulative + 4 * FunctionResult(InputFunction, Xstart + i * TheStep)
Next i
'Loop for even values.
For i = 2 To NumberOfIntervals - 2 Step 2
Cumulative = Cumulative + 2 * FunctionResult(InputFunction, Xstart + i * TheStep)
Next i
'Calculating the final value for Xend.
Cumulative = Cumulative + FunctionResult(InputFunction, Xend)
'Finally, return the result of integration.
SimpsonIntegral = Cumulative * TheStep / 3
Exit Function
'In case of an error show an appropriate message.
ErrorHandler:
SimpsonIntegral = "Unable to calculate the integral of " & InputFunction & "!"
Exit Function
End Function
Private Function FunctionResult(MyFunction As String, x As Double) As Double
'Evaluates a given expression (as a function of xi) for a given xi value.
'Example: FunctionResult("5*xi + 3", 2) returns 5*2 + 3 = 13
'By Christos Samaras
'Date: 23/6/2013
'https://myengineeringworld.net/////
FunctionResult = Evaluate(WorksheetFunction.Substitute(MyFunction, "xi", x))
End Function
In all of the cases that I tried the above function the results were better compared to my previous code. For example, we saw that for the function f(x) = 4*x^2, for x = 0 to 9 the Trapezoidal rule returns the value 978, whereas the composite Simpson’s rule returns 972, which is the correct value:
So, here is another method to calculate the integral of a given expression in Excel. I hope to find it useful.
Download it from here
The file can be opened with Excel 2007 or newer. Please enable macros before using it.
Read also
Numerical Integration In Excel Using The Trapezoidal Rule
Calculating The Area Of A Simple Polygon Using The Shoelace Algorithm