The Shoelace Algorithm For Calculating Polygon’s Area In Excel

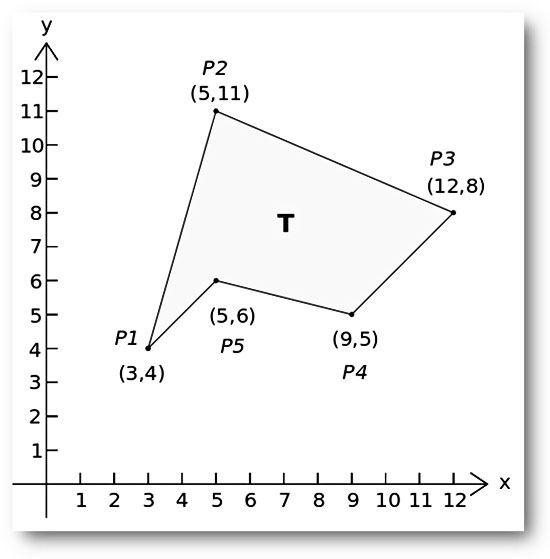
The basics 

It has been quite a while since the last post about mathematical algorithms, so today we will learn how to apply the shoelace algorithm to calculate the area of a simple polygon. First of all, what is the definition of “simple polygon”?

According to Wikipedia: ”In geometry, a simple polygon is defined as a flat shape consisting of straight, non-intersecting line segments or “sides” that are joined pair-wise to form a closed path. If the sides intersect then the polygon is not simple. The qualifier “simple” is frequently omitted, with the above definition then being understood to define a polygon in general. The definition given above ensures the following properties:

• A polygon encloses a region (called its interior) which always has a measurable area.
• The line segments that make up a polygon (called sides or edges) meet only at their endpoints, called vertices or less formally “corners”.
• Exactly two edges meet at each vertex.
• The number of edges always equals the number of vertices.

Two edges meeting at a corner are usually required to form an angle that is not straight (180°); otherwise, the collinear line segments will be considered parts of a single side”.

On the other hand, “the shoelace formula, or shoelace algorithm, is a mathematical algorithm to determine the area of a simple polygon whose vertices are described by ordered pairs in the plane. The user cross-multiplies corresponding coordinates to find the area encompassing the polygon and subtracts it from the surrounding polygon to find the area of the polygon within.

It is called the shoelace formula because of the constant cross-multiplying for the coordinates making up the polygon, like tying shoelaces. It is also sometimes called the shoelace method. It is also known as Gauss’s area formula, after Carl Friedrich Gauss. It has applications in surveying and forestry, among other areas. It is also called the surveyor’s formula”.

The formula can be represented by the expression:

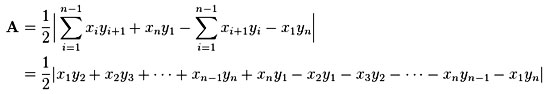
Where:
A: the area of the polygon,
n: the number of sides of the polygon, and
(xi, yi), i = 1, 2,…, n: the vertices (or “corners”) of the polygon.

If you need to apply the shoelace algorithm in Excel, below you will find four different methods! You can choose the one that best fits your needs.

Using the shoelace algorithm in Excel

1st method: Spreadsheet calculations

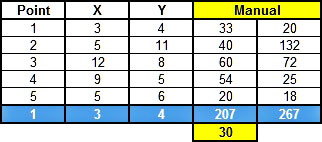
If the points (x, y) of the polygon are known, we can apply the previous equation using simple arithmetical calculations. In this example (taken from Wikipedia) we have 5 points, so, first we calculate the xi*yi+1 (i.e. first point: 3 * 11 = 33 etc.) and then the xi+1*yi (i.e. first point: 5 * 4 = 20 etc.) for each point. Note that for convenience purposes we repeated the coordinates of the first point at the end of the table.

Next, we sum the xi*yi+1 (i.e. 207) and the xi+1*yi (i.e. 267). Finally, we take the absolute value of the difference divided by 2 (i.e. ABS(207 – 267)/2 = 60/2) and the result is the desired polygon area (i.e. 30).

2nd method: SUMPRODUCT formula

With this method, you avoid the intermediate calculations and by using twice the function you get the result. However, the level of difficulty is a little bit higher than the first method (especially if you are new to Excel). The method involves the SUMPRODUCT function, the syntax of which is given below:

SUMPRODUCT(array1, [array2], [array3], …)

The SUMPRODUCT function multiplies the corresponding components in the given arrays and returns the sum of these products. Array1, array2… are the ranges of cells or arrays that you wish to multiply. All arrays must have the same number of rows and columns and you must enter at least 2 arrays (you can have up to 30 arrays).

The difficult part is the array/range definition. If n polygon points (x, y) are known, the function can be written as:

Note that the coordinates of the nth point and the first point must be the same (see the table above), in other words, the polygon should be “closed”. In the sample workbook the SUMPRODUCT function is used with the following ranges:

=0.5*ABS(SUMPRODUCT(C4:C8;D5:D9)-SUMPRODUCT(D4:D8;C5:C9))

In reality, we apply the same function as in the first method, but instead of single cells, we have multiple cells/arrays. Without a doubt, the second method is much more straightforward than the first one.

3rd method: Array formula

This method is a variation of the second one, but instead of SUMPRODUCT functions, we use an array formula. In this example, the following formula is used:

=0.5*ABS(SUM(C4:C8*D5:D9-D4:D8*C5:C9))

Note that after typing an array formula you must press CTRL + SHIFT + ENTER to get the correct result; notice the curly braces “{}” that will enclose your formula. More info about array formulas you can find here.

4th method: Custom VBA function

Open an existing or create a new Excel workbook, switch to the VBA editor (ALT + F11), go to the menu Insert and select Module. In the newly created module (Module1) add the following lines of code.

Option Explicit
 
Function PolygonArea(Xs As Variant, Ys As Variant) As Variant
 
    '-----------------------------------------------------------------------
    'Calculates the area of a simple polygon using the shoelace algorithm.
    'Xs and Ys are the known ordered pairs (x,y) - points of the polygon.
 
    'Written By:    Christos Samaras
    'Date:          25/06/2014
    'E-mail:        [email protected]
    'Site:          https://myengineeringworld.net
    '-----------------------------------------------------------------------
 
    'Declaring the necessary variables.
    Dim i       As Integer
    Dim Area    As Double
 
    'Check if the X values are range.
    If Not TypeName(Xs) = "Range" Then
        PolygonArea = "Xs range is not valid"
        Exit Function
    End If
 
    'Check if the Y values are range.
    If Not TypeName(Ys) = "Range" Then
        PolygonArea = "Ys range is not valid"
        Exit Function
    End If
 
    'Check if the number of X values are equal to the number of Y values.
    If Xs.Rows.Count <> Ys.Rows.Count Then
        PolygonArea = "Number of Xs <> Number of Ys"
        Exit Function
    End If
 
    'Check if there are at least 3 points available (i.e. the polygon is at least triangle).
    If Xs.Rows.Count < 3 Then
        PolygonArea = "You need at least 3 points"
        Exit Function
    End If
 
    'Check if the coordinates of the last points are equal to the coordinates of the first point.
    'In other words, check if the polygon is closed and then apply the shoelace algorithm.
    If Xs(Xs.Rows.Count) = Xs(1) And Ys(Ys.Rows.Count) = Ys(1) Then
        'Polygon is closed (last point = first point).
        For i = 1 To Xs.Rows.Count - 1
            Area = Area + (Xs(i + 1) + Xs(i)) * (Ys(i + 1) - Ys(i))
        Next i
    Else
        'The polygon is not considered closed.
        For i = 1 To Xs.Rows.Count - 1
            Area = Area + (Xs(i + 1) + Xs(i)) * (Ys(i + 1) - Ys(i))
        Next i
        'Use the coordinates of the first point to "close" the polygon.
        Area = Area + (Xs(1) + Xs(Xs.Rows.Count)) * (Ys(1) - Ys(Ys.Rows.Count))
    End If
 
    'Finally, calculate the polygon area.
    PolygonArea = Abs(Area / 2)
 
End Function 

The VBA function is quite simple in use. The user just enters two ranges that contain the X and Y coordinates of the polygon points/vertices and the code automatically calculates the enclosed area. Moreover, the function incorporates some basic error handling, so, if the input ranges have an error, the function will display an error message to the user.

Limitations of shoelace algorithm

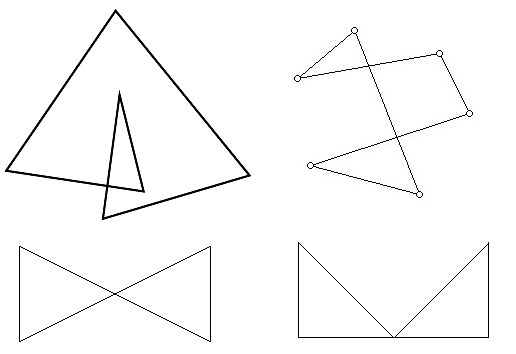
As mentioned earlier, the shoelace algorithm works ONLY with a SIMPLE POLYGON. Consequently, if the polygon crosses or overlaps itself the algorithm will fail. Thus, if your polygon is similar to any of the polygons shown in the above picture do NOT apply any of the presented methods of shoelace algorithms. The results will be INACCURATE.

Downloads

The file can be opened with Excel 2007 or newer. Please enable macros before using it.

Read also

Numerical Integration In Excel Using The Trapezoidal Rule
Numerical Integration In Excel Using The Composite Simpson’s Rule